I do thank you for your support and interest in my work. It is kind of fun putting these news letters together because I enjoy writing about my ideas and sharing some of these thought with you. I hope you will feel free to email me back and give me your thoughts on some of these ideas.
Streets of a Story CD Release Concert
I want to start this news letter off with some information on my son Lang Termes. I am very proud of what he has done with his music career. Not only is he finding steady gigs in Bozeman Montana but also creating 80% of the music he plays. I am pleased he sees the difference in playing what the world has already accepted and trying to find new paths. I know this is a much harder path to travel but in the end it is much more rewarding.
Lang will be coming back to the Hills for a CD Release Concert at the Dahl Fine Arts Center in Rapid City on the 15th of April at 1:30. I hope any of you that can make it will come to this gathering and if you can’t, go to his website and listen to parts of these songs or buy his latest CD. Hope to see you there. This is his concert poster.
Explaining Some of My Older Ideas
CAPTURED WORLD POLYHEDRA
When I created these polyhedron paintings, my interest was in getting the concept of the six-point perspective into a reproducible form. At that time I wasn’t able to reproduce the spherical paintings as spheres so the best next thing was to flatten the spheres into polyhedron so they could be reproduced.
I wanted a similar concept to be on these polyhedra as was on the sphere. I also wanted the six-point perspective to look like it belonged on the different polyhedron. This meant I wanted the geometry of the perspective to fit with the geometry of the polyhedron. How do you get six equal distant points to fit in a sound way on the five regular polyhedron? The six equal distant points that I use on the sphere geometrically are equal to the six points or vertices of the octahedron. The Octahedron is a polyhedron that has eight equilateral triangles which make up its faces and these triangles come together into six junctions or vertices. My job was to see how these six points would fit into the other four regular polyhedra. After some study I found they do. I found out many people already knew they fit together but none of them were getting them to fit so that their drawing would look good so, at least got to that point first. In making this study I learned a great deal of new information on just how exciting the study of polyhedron was. It has turned into a couple of different workshops I offer to math and art classes. The following are examples of what I got from this thinking.
CUBE WITH FOUR (THREE TWISTED) MOEBIUS INSIDE
I created this sculpture around 1972. It was made from one inch metal cubical tubing welded together to make a stable two foot cube. From one corner a rod was welded so it could be displayed from a corner as the bottom. Holes were then drilled into the metal about an eight of an inch apart. Clear plastic line was woven into these holes and stretched around to three different edges of the cube. These three edges were going in three different directions, Up and down, north and south and east and west. The result was three bands of these triple twisted patterns floating inside the cube. I only strung these lines from the center one third of the edges of the cube. Something special goes on with the geometry because not one of the patterns created from this touched each other. My question to this day is, would this not touching have happened if I would have continued each of these bands out to the corners?
This three twisted band which three are in this cube led me into another form I played with. Adding a little dimension to this band turns it into what is called the Penrose Tribar. (see illustration) This is an illusion that Roger Penrose invented and M.C. Escher explored. The Penrose Tribar is an impossible structure only possible as a drawing. Escher played with this structure when he created ASCENDING AND DESCENDING which shows people going up a stairway and coming right back to the bottom even though the people have gone only up the stairs. WATERFALL also uses the Tribar to show waterfalls that fall and fall but somehow come back to where they began.
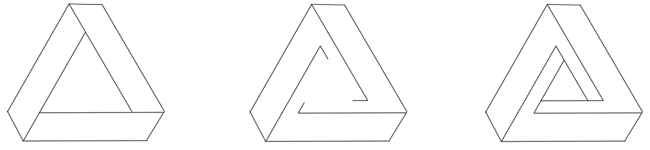I would like to make a comparison with this impossible cubical structure. The drawing below shows how I progress from this cubical structure to an impossible cylinder structure. What do you think? Is it the same illustration except in cylinder form?
Why I enjoy painting on Spheres
I get asked, “Are you still painting on spheres?” a lot. I guess some people think I am just going in circles. Here is my comment to them.
Think about how many paintings have been done on the flat surface over the past 2000 years. They have covered and recovered that flat surface pretty well. If you think just on the geometrical level of the difference between the flat surface and the sphere surface you will realize there is a lot of difference. The patterns, which fit on the flat, will not fit the same way on the sphere. So the sphere offers a whole different set of ideas which are not possible on the flat. Therefore, I would guess there are at least 2000 years of spherical painting ideas possible.
New spheres just finished
THE OLD BALL GAME
This piece was finished and hung in Alyce Schavones’ home in Spearfish South Dakota. Alyce had a opening for her sphere February 24th. Going along with the Wrigley Field theme we had the proper beer and hotdogs at the gathering. We had a great time at this unique and fun opening.
What I am working on
It is in an early stage but it should be a most interesting concept.
The room you are in is painted with opaque paint so you can’t see through it except there are lots of mirrors on the walls of the room. All of the mirrors are left transparent. When you look into the mirrors you are looking at the back-side of the sphere. The back-side of the sphere is conceptually what is behind you so the mirror is reflecting that. There are enough mirrors to let light into the inside of the sphere to allow it to show up when seen through the mirror.
Where I have been lately
CREATIVE CONNECTIONS was just completed. This was the fourth time I was invited to Oberwessel Germany to work with 15 arts students from the DoDDS-Europe. 150 fine arts students are picked from 35 High Schools. Theater, music, and the visual arts have a variety of areas they can study.
GALLERY SHOWINGS OF TERMESPHERES This last month I showed 22 Termespheres and did workshops at the CAMPLEX CENTER in Gillette Wyoming. This show was up until March 3rd. The reception for this show was February 23rd. This was a wonderful place to show and great people to work with.
I also just finished a workshop and showing with the Math Department at WESTERN WASHINGTON UNIVERSITY in Bellingham Washington. I tied together slides of my work with the workshop of one through six-point perspective. I think it went over very well. I was also pleased that they gave each of the participants the book I have a chapter in called Masters of Deception by Al Seckel.
I JUST SOLD A SPHERE TO the GLASGOW SCIENCE MUSEUM in Scotland. The lady there saw a Termesphere in the SINGAPORE SCIENCE MUSEUM and said she couldn’t get it out of her mind. Singapore has the FISH EYE VIEW and Glasgow will have THE HUMAN CAGE. The Singapore Science Museum has an optical illusion permanent show which has my sphere in it. I also have a sphere in The Discovery Museum in Acton Mass. So the Science Museums are showing quite in interest in my work.
PENROSE TRIBAR SPHERE just sold to Tom Rogers from Atlanta Georgia. He is the organizer of the Gardner Conferences there and is a very good friend of Roger Penrose.
Thank you for reading to the end
I hope some of my thoughts will get some comments back from you, positive or negative and, new ideas.
I love the way some of my math friends are making suggestions of concepts for me to consider. If you would like to be taken off this newsletter list please let me know. As always, thank you for your tremendous support and encouragement. I would love to hear what you think.
Feel free to call at 888-642-4805 or email me termes@blackhills.com