CAPTURED WORLD POLYHEDRA

When I created these polyhedron paintings, my interest was in getting the concept of the six-point perspective into a reproducible form. At that time I wasn’t able to reproduce the spherical paintings as spheres so the best next thing was to flatten the spheres into polyhedron so they could be reproduced. I wanted a similar concept to be on these polyhedra as was on the sphere. I also wanted the six-point perspective to look like it belonged on the different polyhedron. This meant I wanted the geometry of the perspective to fit with the geometry of the polyhedron. How do you get six equal distant points to fit in a sound way on the five regular polyhedron? The six equal distant points that I use on the sphere geometrically are equal to the six points or vertices of the octahedron. The Octahedron is a polyhedron that has eight equilateral triangles which make up its faces and these triangles come together into six junctions or vertices. My job was to see how these six points would fit into the other four regular polyhedra. After some study I found they do. I found out many people already knew they fit together but none of them were getting them to fit so that their drawing would look good so, at least got to that point first. In making this study I learned a great deal of new information on just how exciting the study of polyhedron was. It has turned into a couple of different workshops I offer to math and art classes. The following are examples of what I got from this thinking.
CUBE WITH FOUR (THREE TWISTED) MOEBIUS INSIDE

I created this sculpture around 1972. It was made from one inch metal cubical tubing welded together to make a stable two foot cube. From one corner a rod was welded so it could be displayed from a corner as the bottom. Holes were then drilled into the metal about an eight of an inch apart. Clear plastic line was woven into these holes and stretched around to three different edges of the cube. These three edges were going in three different directions, Up and down, north and south and east and west. The result was three bands of these triple twisted patterns floating inside the cube. I only strung these lines from the center one third of the edges of the cube. Something special goes on with the geometry because not one of the patterns created from this touched each other. My question to this day is, would this not touching have happened if I would have continued each of these bands out to the corners? This three twisted band which three are in this cube led me into another form I played with. Adding a little dimension to this band turns it into what is called the Penrose Tribar. (see illustration) This is an illusion that Roger Penrose invented and M.C. Escher explored. The Penrose Tribar is an impossible structure only possible as a drawing. Escher played with this structure when he created ASCENDING AND DESCENDING which shows people going up a stairway and coming right back to the bottom even though the people have gone only up the stairs. WATERFALL also uses the Tribar to show waterfalls that fall and fall but somehow come back to where they began. 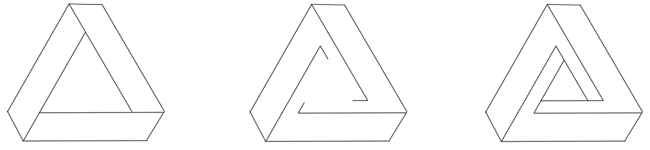 I would like to make a comparison with this impossible cubical structure. The drawing below shows how I progress from this cubical structure to an impossible cylinder structure. What do you think? Is it the same illustration except in cylinder form?
I would like to make a comparison with this impossible cubical structure. The drawing below shows how I progress from this cubical structure to an impossible cylinder structure. What do you think? Is it the same illustration except in cylinder form? 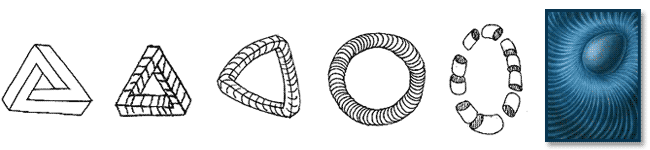
Comments 1
I want to know if people see this the way I do. The Penrose Tribar is a cubical impossible structure. I think the cylinder structure I play with is the same impossible structure but it is in the arrangement of cylinders rather than cubes.